보어 모형
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
보어 모형은 1913년 닐스 보어가 제안한 원자 모형으로, 전자가 특정 궤도에서만 안정적으로 공전하며 궤도 간 전이 시 에너지를 흡수 또는 방출한다는 가정을 도입했다. 이 모형은 러더퍼드의 원자 모형의 문제점을 해결하고 수소 원자의 스펙트럼을 설명하기 위해 개발되었으며, 각운동량의 양자화 조건을 통해 에너지 준위를 계산했다. 보어 모형은 뤼드베리 공식을 유도하고 무거운 원자의 껍질 모델을 제시하는 데 기여했으며, 모즐리의 법칙을 통해 원자 번호의 객관적인 의미를 확립하는 데 중요한 역할을 했다. 하지만, 보어 모형은 전자의 타원 궤도를 도입한 좀머펠트 모형과 마찬가지로 근본적인 불일치와 한계점을 가지고 있었고, 결국 현대적인 양자 역학으로 대체되었다.
더 읽어볼만한 페이지
- 닐스 보어 - 오게 닐스 보어
오게 닐스 보어는 덴마크의 물리학자이자 닐스 보어의 아들로, 원자핵 구조 이론 연구로 노벨 물리학상을 수상했으며 코펜하겐 대학교 교수와 닐스 보어 연구소 소장을 역임하며 원자핵 물리학 분야에 큰 업적을 남겼다. - 닐스 보어 - 보어 마그네톤
보어 마그네톤은 전자의 자기 쌍극자 모멘트의 자연 단위로, 원자나 분자의 자기적 성질을 기술하는 데 사용되는 기본 상수이며, 닐스 보어가 도출하고 볼프강 파울리가 명명했으며, 전자의 전하량, 환산 플랑크 상수, 전자 질량으로 정의된다. - 1913년 과학 - 테라노바 원정
테라노바 원정은 1910년부터 1913년까지 로버트 팰컨 스콧이 이끈 영국의 남극 탐험으로, 남극점 정복 경쟁과 과학 연구를 목표로 했으나 스콧을 포함한 탐험대원 전원이 귀환 중 사망하는 비극과 스콧의 리더십에 대한 논쟁을 남겼다. - 1913년 과학 - 파섹
파섹은 천문학에서 별까지의 거리 측정에 사용되는 단위로, 1각초의 연주 시차를 가지는 거리에 해당하며 약 3.26광년 또는 30.86조 킬로미터이고, 천체의 거리에 따라 킬로파섹, 메가파섹 등으로 표현되며 다양한 천문학적 거리 척도에 사용된다. - 부정된 과학 이론 - 생기론
생기론은 생명체에 물리화학적 과정으로 설명 안 되는 특수한 생명력이나 원리가 있다는 이론으로, 고대 그리스에서 시작되어 근대 과학 발전에 대한 반작용으로 부각되었으나, 기계론적 생물학 발전으로 과학계에서 널리 받아들여지지 않지만 일부 대체의학이나 철학, 종교적으로 논의된다. - 부정된 과학 이론 - 태양중심설
태양중심설은 행성들이 태양을 중심으로 공전한다는 이론으로, 아리스타르코스가 최초로 제기했으나 코페르니쿠스에 의해 부활되었고, 케플러, 갈릴레이, 뉴턴 등에 의해 과학적 사실로 확립되었지만, 현대에는 태양계 질량중심을 기준으로 하며 태양이 특별한 위치를 차지하지 않는다는 것이 밝혀졌다.
2. 기원 및 역사
20세기 초, 어니스트 러더퍼드의 실험은 작고 빽빽하며 양전하를 띤 원자핵 주위를 음전하의 전자 구름이 감싸는 형태의 원자 개념을 정립하였다.[52] 러더퍼드는 이 실험 데이터를 바탕으로 1911년에 태양계와 유사한 원자 모형을 제안했지만, 이 모형은 심각한 기술적 문제점을 안고 있었다. 고전 물리학에 따르면, 전자가 핵 주위를 공전하면서 전자기 복사를 방출하여 에너지를 잃고, 결국 약 16피코초 만에 핵과 충돌하여 모든 원자가 매우 불안정한 상태가 된다는 것이다.[53][54] 또한, 전자가 핵으로 빨려 들어가면서 궤도가 작아지고 공전 주기가 빨라져 연속적으로 증가하는 진동수의 전자기 복사를 방출할 것이라고 예측되었지만, 19세기 말의 전기 방전 실험에서는 원자가 특정한 주파수에서만 전자기파를 방출하는 이산적인 현상이 관찰되었다.
이러한 한계를 극복하기 위해 1913년 닐스 보어는 전자가 특정한 움직임만 가질 수 있다는 가정을 바탕으로, 현재 보어의 원자 모형으로 불리는 새로운 모형을 제시했다. 보어 모형의 핵심은 다음과 같다.
# 원자 내 전자는 핵을 중심으로 공전하며, 이 때 전기적인 인력이 구심력 역할을 한다.
# 전자는 핵으로부터 특정한 거리에서만, 즉 정상 상태라고 불리는 특정한 궤도에서만 전자기 복사를 방출하지 않고 안정적으로 공전한다. 이 궤도들은 에너지 껍질 또는 에너지 준위라고 불리며, 불연속적인 에너지 값을 갖는다.
# 전자는 한 궤도에서 다른 궤도로 전이할 때만 에너지를 흡수하거나 방출하며, 이때 흡수 또는 방출되는 진동수는 플랑크-아인슈타인 관계식에 따라 결정된다.
보어 모형의 중요성은 전자의 움직임을 설명하기 위해 고전 역학에 양자 조건을 도입했다는 점에 있다. 보어는 전자의 각운동량이 특정 단위의 정수배여야 한다는 양자 규칙을 이용하여 에너지 준위 간의 간격을 계산했다.
:
여기서 n은 주 양자수를 나타내며, 1, 2, 3 등의 값을 갖는다. n의 최솟값은 1이며, 이는 0.0529nm의 가장 작은 궤도 반지름을 나타내며, 보어 반지름이라고도 한다.
보어 모형은 다음과 같은 특징을 갖는다.
# 알베르트 아인슈타인의 광전 효과처럼, 보어의 공식은 양자 전이 시 에너지가 불연속적으로 방출된다고 가정한다. 그러나 보어는 광자의 존재를 믿지 않고, 전자기장의 양자화를 원자 에너지 준위의 불연속성으로 설명했다.[55][56]
# 맥스웰 이론에 따르면, 고전적인 복사의 진동수는 궤도에서 정상파를 이루는 전자의 공전 진동수와 같다.
# 보어-크래머-슬래이터 이론은 보어 모형을 확장하려는 시도였으나, 양자 전이 과정에서 에너지 보존 법칙과 운동량 보존 법칙을 위배한다는 문제점을 드러냈다.
1924년, 루이 드 브로이는 전자가 파동으로 묘사될 수 있으며, 전자 궤도의 둘레는 파장의 정수배여야 한다는 정상파 조건으로 보어의 조건을 재해석했다.
:
드 브로이 파장 식을 통해 보어의 규칙을 유도할 수 있다. 그러나 1913년 당시 보어는 자신의 모형을 파동적 해석으로 설명하지 않았다.
1925년에는 양자 역학이라는 새로운 종류의 역학이 제시되었다. 베르너 하이젠베르크가 제시한 이 이론은 양자화된 전자의 움직임을 설명하는 보어 모형을 보다 정확한 형태로 확장했다. 에르빈 슈뢰딩거는 드 브로이의 물질파 이론을 도입하여 독자적으로 파동 역학을 확립했다.
2. 1. 톰슨의 원자 모형 (건포도 푸딩 모형)
보어가 1912년 여름 새로운 원자 이론 연구를 시작했을 때, 가장 유력한 원자 모형은 J J 톰슨이 제안한 건포도 푸딩 모형이었다.[6] 톰슨은 양전하가 원자 크기의 구형 부피에 퍼져 있고, 그 안에 전자들이 동일 평면 고리 모양으로 회전한다고 제안했다. 톰슨은 오랜 계산을 통해 이 모형이 기계적으로 안정적이며, 원자 당 수천 개의 전자라는 초기 가정 하에 전기역학적으로도 안정적임을 보였다. 더욱이 그는 고리 모양으로 특히 안정적인 전자 배열이 원자의 화학적 특성과 관련이 있다고 제안했다. 그는 베타 입자 산란에 대한 공식을 개발했는데, 이는 실험 결과와 일치하는 듯했다.[6]그러나 톰슨 자신도 나중에 원자가 그보다 1000배 적은 전자를 가지고 있음을 보여주었고, 이는 안정성 논증에 의문을 제기하고, 이해가 부족한 양전하 구체가 원자 질량의 대부분을 차지해야 한다는 것을 강요했다. 톰슨은 또한 원자 스펙트럼의 많은 선들을 설명할 수 없었다.[9]
2. 2. 러더퍼드의 핵 모형
어니스트 러더퍼드는 1911년에 알파 입자 산란 실험을 통해 원자 중심에 작고 밀도가 높은 양전하를 띤 핵이 존재함을 밝혔다. 이 실험 데이터를 바탕으로 러더퍼드는 태양계와 유사한 원자 모형을 제안했다. 하지만 이 모형은 전자가 핵 주위를 공전하면서 전자기 복사를 방출하여 에너지를 잃고 핵으로 빠르게 충돌한다는 고전 물리학 법칙과 맞지 않는 기술적인 문제가 있었다. 또한, 전자의 궤도가 안쪽으로 말려들어오면서 궤도가 작아지고 공전 주기가 빨라져 연속적으로 증가하는 진동수의 전자기 복사를 방출할 것이라는 예측과 달리, 실제 전기 방전 실험에서는 원자가 특정한 주파수에서만 전자기파 복사를 방출하는 이산적인 현상이 관찰되었다.[52][53][54]러더퍼드의 원자 모형은 전자를 포함하지 않아 불완전했지만,[7] 닐스 보어는 핵 주위를 도는 전자의 개념을 도입하여 자신의 모형을 발전시켰다.[8]
2. 3. 원자 스펙트럼
20세기 초, 원자 스펙트럼은 요한 발머와 요하네스 리드베리에 의해 경험적 공식으로 요약되었지만, J. J. 톰슨이 제안한 건포도 푸딩 모형[6] 등 당시의 원자 모형으로는 설명할 수 없었다.[9] 리드베리-리츠 결합 원리는 원자 스펙트럼 선 주파수를 각 원소의 특징적인 주파수인 '항' 사이의 차이와 관련시켰다.[26] 보어는 이러한 항들을 플랑크 상수로 나눈 원자의 에너지 준위로 인식하여, 스펙트럼 선이 에너지 차이로 인해 발생한다는 현대적 관점으로 이어졌다.[12][13]2. 4. 솔베이 회의의 영향
1911년에 열린 제1차 솔베이 회의는 최초의 국제 물리학 회의 중 하나였다. 닐스 보어의 스승인 어니스트 러더퍼드를 포함하여 9명의 노벨상 수상자 또는 미래의 노벨상 수상자들이 참석했다.[17] 보어는 참석하지 않았지만 솔베이 회의 보고서를 읽었고[14] 러더퍼드와 논의했다.[15]회의의 주제는 막스 플랑크의 진동자의 복사 이론과 에너지 양자였다.[16] 플랑크는 회의에서 원자에 대한 논평으로 강연을 마쳤고, 그 후 이어진 토론은 원자 모형에 관한 것이었다. 헨드릭 로렌츠는 하스(Haas)의 모형을 바탕으로 원자의 구성에 대한 질문을 제기했다. 로렌츠는 하스가 했던 것처럼 원자의 크기를 이용하여 플랑크 상수를 결정하거나, 플랑크 상수를 이용하여 원자의 크기를 결정할 수 있다고 설명했다.[17] 보어는 후자의 방법을 채택하게 된다.
토론은 원자에 양자 이론을 포함해야 할 필요성을 강조했다. 플랑크는 고전 역학의 결함을 명시적으로 언급했다.[17] 보어는 이미 그의 박사 학위 논문에서 유사한 의견을 표명했지만, 솔베이 회의에서 당대 최고의 과학자들은 고전 이론과의 결별에 대해 논의했다.[15] 보어의 원자 모형에 관한 첫 번째 논문은 솔베이 회의록을 인용하며 다음과 같이 말한다. "전자의 운동 법칙이 어떻게 변하든, 문제의 법칙에 고전 전자기학에는 없는 양, 즉 플랑크 상수(현대적인 표현은 "플랑크 상수"이지만, 이는 직접 인용이다) 또는 종종 작용의 기본 양자라고 불리는 양을 도입하는 것이 필요해 보인다."[8] 솔베이 회의의 논의에 고무된 보어는 원자가 안정적이라고 가정하고 원자의 고전적 모형을 안정화하려는 노력을 포기한다.[26]
2. 5. 니콜슨의 원자 이론
1911년 존 윌리엄 니콜슨은 보어 모형에 영향을 미칠 원자 모형을 발표했다. 니콜슨은 천체 물리학적 분광 분석을 기반으로 자신의 모형을 개발했다. 그는 관측된 스펙트럼 선 주파수를 원자 내 전자의 궤도와 연결했다. 그가 채택한 연결은 원자 전자 궤도 각운동량을 플랑크 상수와 연관시켰다. 플랑크가 에너지 양자에 초점을 맞춘 반면, 니콜슨의 각운동량 양자는 궤도 주파수와 관련이 있었다. 이 새로운 개념은 플랑크 상수에 최초로 원자적 의미를 부여했다.[18] 1913년 논문에서 보어는 니콜슨을 인용하며 원자에 중요한 양자화된 각운동량을 발견했다고 언급한다.[8]니콜슨 연구의 또 다른 중요한 영향은 스펙트럼에 대한 그의 상세한 분석이었다. 니콜슨의 연구 이전에 보어는 스펙트럼 데이터가 원자를 이해하는 데 유용하지 않다고 생각했다. 보어는 자신의 연구를 니콜슨의 연구와 비교하면서 스펙트럼 데이터와 그 가치를 이해하게 되었다. 그 후 친구로부터 발머 공식에 대해 알게 된 보어는 자신의 모형이 그것과 자세히 일치한다는 것을 깨달았다.[18]
니콜슨의 모형은 J.J. 톰슨의 건포도 푸딩 모형과 같은 맥락에서 고전 전자기학을 기반으로 했지만, 구형 내에서 순환하는 대신 양성자 핵 주위를 도는 음전자를 가졌다. 이 시스템의 즉각적인 붕괴를 피하기 위해 그는 전자가 쌍으로 존재해야 하며, 각 전자의 회전 가속도가 궤도 전체에서 일치해야 한다고 주장했다.[18] 1913년까지 보어는 알파 입자 에너지 손실 분석을 통해 수소가 쌍이 아닌 단일 전자만 가지고 있음을 이미 보여주었다.[26] 보어의 원자 모형은 고전 전자기학을 버리게 되었다.
니콜슨의 복사 모형은 양자적이었지만 전자의 궤도와 연결되었다.[19][16] 보어의 양자화는 궤도 주파수가 아니라 수소 모형의 에너지 준위 차이와 관련이 있었다.
3. 전자의 에너지 준위
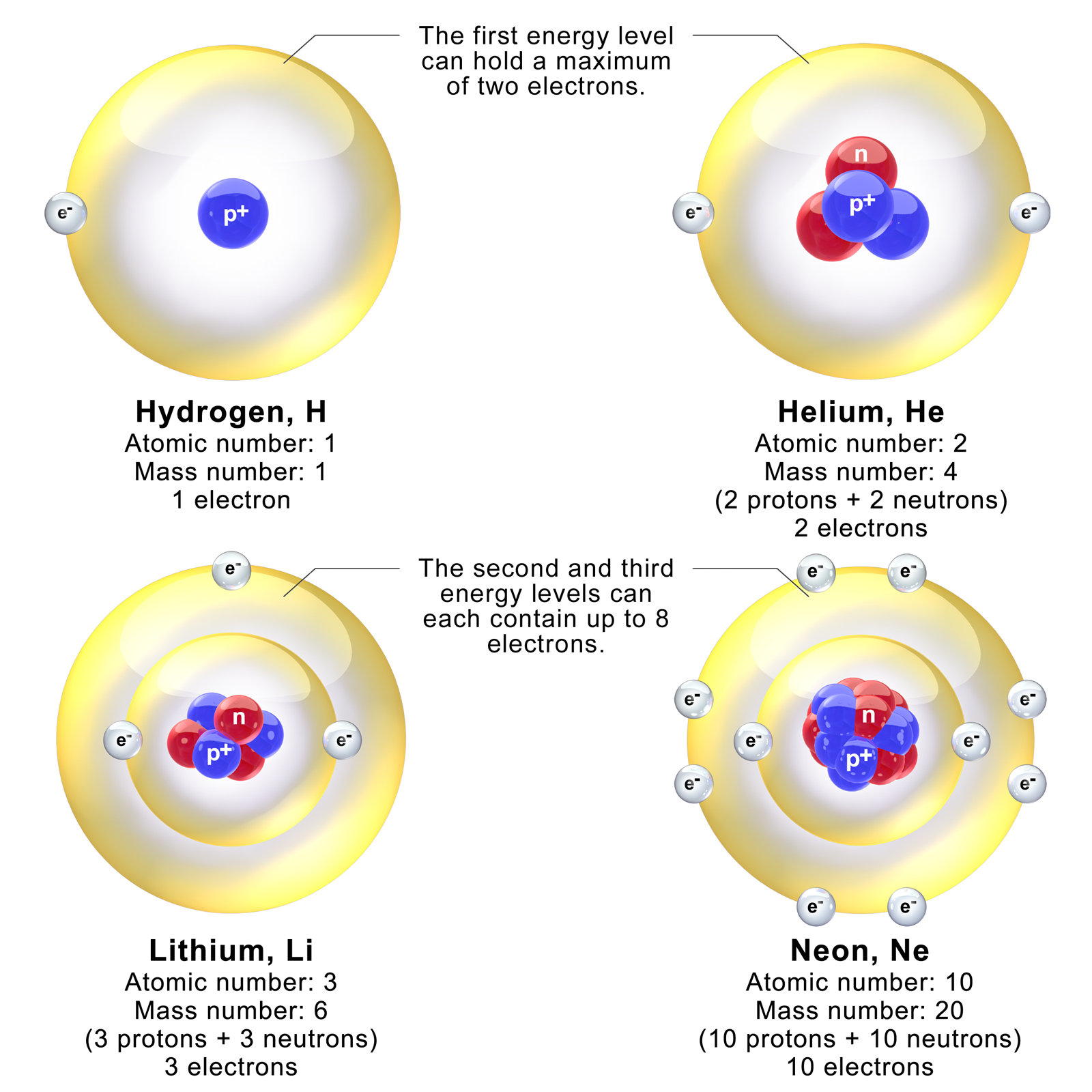
보어 모형은 수소 원자, 헬륨 이온(He+), 리튬 이온(Li2+)과 같이 전자가 하나인 시스템에서 정확한 결과를 제공한다.[8] 또한 포지트로늄과 같이 하나의 전자가 다른 모든 것으로부터 멀리 떨어진 뤼드베리 상태에서도 적용된다.
보어 모형에서 전자의 에너지 준위는 다음과 같이 주어진다.
:
여기서 Z는 원자 번호, RE는 뤼드베리 에너지, n은 주양자수이다. 뤼드베리 에너지는 다음과 같이 표현된다.
:
이 식에서 ke는 쿨롱 상수, e는 전하의 기본 전하량, me는 전자의 질량, ħ는 플랑크 상수(h)를 2π로 나눈 값이다.
뤼드베리 에너지는 전자의 정지 질량 에너지(, 511 keV)와 미세구조상수()를 통해 다음과 같이 표현할 수 있다.
:
수소 원자(Z=1)의 경우, 전자는 가장 낮은 에너지 준위(n=1)에서 약 -13.6eV의 에너지를 가지는데, 이는 핵으로부터 무한히 떨어진 정지한 전자보다 낮은 에너지이다. n값이 커질수록 에너지 준위는 높아지며, 이는 전자가 원자핵에서 더 멀리 떨어진 궤도를 돌고 있음을 의미한다.
보어 모형은 전자가 원자핵 주위를 돌면서 에너지를 잃지 않고 특정 궤도에서만 존재할 수 있다는 양자 조건을 도입하여, 원자의 안정성과 불연속적인 에너지 준위를 설명한다.
3. 1. 전자의 에너지 준위 유도
보어는 고전 역학과 양자 역학의 가정을 결합하여 전자의 에너지 준위를 유도했다.[8]:
:여기서 ''m''e는 전자의 질량, ''e''는 기본 전하량, ''k''e는 쿨롱 상수, ''Z''는 원자의 원자 번호이다. 핵의 질량은 전자 질량보다 훨씬 크다고 가정한다. 이 방정식은 임의의 반지름에서 전자의 속도를 결정한다.
::
:또한 임의의 반지름에서 전자의 총에너지를 결정한다.
::
:총에너지는 음수이며 ''r''에 반비례한다. 이는 궤도 전자를 양성자로부터 끌어내는 데 에너지가 필요함을 의미한다. ''r''의 값이 무한대일 때, 에너지는 0이 되며, 이는 양성자로부터 무한히 멀리 떨어진 정지 상태의 전자에 해당한다. 총에너지는 퍼텐셜 에너지의 절반이며, 차이는 전자의 운동 에너지이다. 이것은 비리얼 정리에 의해 비원형 궤도에도 해당한다.
- 양자 규칙: 각운동량 은 ''ħ''의 정수배이다.
::
속도에 대한 식을 대입하면 ''n''에 대한 ''r''의 방정식이 주어진다.
:
따라서 허용되는 궤도 반지름은 임의의 ''n''에 대해 다음과 같다.
:
수소 원자(Z = 1)에서 가능한 가장 작은 ''r'' 값을 보어 반지름이라고 하며 다음과 같다.
:
임의의 원자에 대한 ''n''번째 준위의 에너지는 반지름과 양자수에 의해 결정된다.
:
따라서 수소(n = 1)의 가장 낮은 에너지 준위에 있는 전자는 핵으로부터 무한히 먼 곳에 정지해 있는 전자보다 약 13.6 eV 낮은 에너지를 갖는다. 다음 에너지 준위(n = 2)는 −3.4 eV이고, 세 번째(n = 3)는 −1.51 eV 등이다. ''n'' 값이 클수록 이것은 원자의 나머지 부분 주위의 큰 원형 궤도에 전자가 하나 있는 고도로 여기된 원자의 결합 에너지이기도 하다.
에너지 공식의 자연 상수 조합을 리드베리 에너지(''R''E)라고 한다.
:
이 표현은 더 많은 자연 단위를 형성하는 조합으로 해석하여 명확하게 한다.
- 는 전자의 정지 질량 에너지(511 keV)이다.
- 는 미세 구조 상수이다.
- .
''Z'' = 1/''α'' (''Z'' ≈ 137)인 경우 운동이 매우 상대론적이 되고 ''Z''2는 ''R''의 ''α''2를 상쇄한다. 궤도 에너지는 정지 에너지와 비교할 수 있게 된다. 충분히 큰 핵은 안정적이라면 진공으로부터 결합된 전자를 생성하여 양전자를 무한대로 방출함으로써 전하를 감소시킨다.
보어 공식은 전자 질량 대신 모든 상황에서 전자와 양성자의 환산 질량을 적절히 사용한다.
:
그러나 이 숫자는 양성자의 질량이 전자 질량보다 훨씬 크기 때문에(약 1836.1배) 거의 같다.
4. 뤼드베리 공식
뤼드베리 공식은 보어의 이론 이전에 이미 알려진 공식으로, 오비탈 간 에너지 준위 차이로 발생하는 양자 도약 또는 에너지 전이를 설명한다. 보어 공식은 플랑크 상수와 전자의 전하를 포함한 이미 잘 알려진 자연 상수들로 뤼드베리 상수를 표현하여 수치를 제공한다.[28][29] 전자가 높은 에너지 상태에서 낮은 에너지 상태로 이동할 때 양자가 방출되는데, 이때 방출되는 빛의 파장은 뤼드베리 공식으로 결정된다.
::
여기서 nf는 나중 에너지 준위, ni는 처음 에너지 준위, R은 뤼드베리 상수이다.
19세기 분광학 연구 과학자들은 이 공식을 이미 알고 있었지만, 보어 이전까지는 이론적인 설명이나 R값의 예측이 불가능했다. 보어는 자신의 모델을 통해 뤼드베리 상수를 유도하고, 실험적으로 관측된 라이먼, 발머, 파셴 계열의 스펙트럼 선과 일치하는 결과를 얻었다. 또한 아직 관측되지 않은 다른 선들도 성공적으로 예측하여 그의 모델이 즉시 받아들여지는 데 기여했다.[29]
보어는 그의 친구 한스 한센(Hans Hansen)으로부터 발머 계열이 1885년 요한 발머(Johann Balmer)가 발견한 발머 공식(Balmer formula)을 사용하여 계산된다는 것을 알게 되었다.[14][20] 이것은 1888년 요하네스 뤼드베리(Johannes Rydberg)에 의해 일반화되어 현재 뤼드베리 공식(Rydberg formula)으로 알려져 있으며, 보어는 "모든 것이 명확해졌다"고 선언했다.[20]
5. 무거운 원자의 껍질 모델
보어는 수소 원자 모델을 확장하여 무거운 원자에 대한 대략적인 모델을 제시했다. 무거운 원자들은 원자핵 안에 많은 양성자를 가지고, 그 전하를 상쇄시키기 위한 더 많은 전자들을 가진다. 보어는 각 궤도가 특정한 수의 전자만을 수용할 수 있으며, 그 궤도가 채워지면 다음 궤도가 사용된다는 껍질 구조를 가정했다.[3]
이러한 모델은 가리움 효과를 통해 전자들 간의 상호작용을 설명한다. 바깥 궤도에 있는 전자들은 원자핵 뿐만 아니라, 내부 전자 주변을 운동한다. 따라서 그들이 느끼는 실질적인 전하 Z는 내부 궤도의 전자들의 수에 의해 감소된다.
예를 들어, 리튬 원자는 가장 낮은 1s 궤도에 2개의 전자를 가지고 Z=2에서 이러한 궤도를 가진다. 각각의 전자는 Z=3의 핵 전하가 다른 전자들의 가리움 효과를 상쇄시키는 것을 보여주는데, 이는 약 1단위의 핵 전하를 감소시킨다. 리튬에서 가장 바깥쪽 전자는 Z=1에서 궤도운동을 하는데, 이는 두 내부 전자들이 약 2정도의 핵 전하를 감소시키기 때문이다.
모즐리의 법칙은 실험적으로 가장 안쪽 전자쌍들을 조사하여, 그들이 대략적으로 Z-1의 핵 전하를 보일 수 있음을 보여주었다. 반면에, 가장 바깥 껍질에 오직 하나의 전자를 가진 원자나 이온에서 가장 바깥쪽 전자는 Z-k라는 실질적인 전하를 가지는 속 궤도를 회전하는데, 이 때 k는 내부 껍질에 있는 전자들의 전체 수이다.
껍질 모델은 19세기 후반까지 원소 주기율표 상에서 암호화되어 있던 많은 원자의 특성들을 질적으로 설명해줄 수 있다. 원자들은 주기율표 상에서 오른쪽으로 갈수록 더 작아지려는 경향이 있고, 다음 주기로 갈수록 더 커지려는 경향이 있다. 주기율표의 오른쪽에 있는 원자들은 전자를 얻으려는 경향이 있는 반면, 왼쪽에 있는 원자들은 그것들을 잃어버리려는 경향이 있다. 주기율표의 마지막 족의 원소들은 화학적으로 불활성기체들이다.
껍질 모델에서, 이러한 현상은 껍질 채움에 의해 설명된다. 왜냐하면 그들은 그 궤도가 다 찰 때까지 같은 크기의 궤도를 채우고 있기 때문인데, 이는 주기율표 상에서 그 다음 원자가 전자 간의 반발력에 의해 그것이 팽창됨을 야기함에 따라 바깥 전자를 느슨히 구속하고 있음을 의미한다. 첫 번째 보어 궤도는 그것이 두 개의 전자를 가질 때 가득 채워 지는데, 이는 왜 헬륨이 비활성인지를 설명한다. 두 번째 궤도는 8개의 전자를 수용하고, 그것이 꽉 채웠을 때 원자가 네온인데, 이 역시 비활성이다.
6. 모즐리의 법칙과 K-alpha X-ray 방출선 계산
헨리 모즐리는 원자에서 방출되는 가장 강한 X선(K-알파 선)과 원자 번호 사이의 관계(모즐리의 법칙)를 발견했다.[57] 이 법칙은 요한네스 뤼드베리와 닐스 보어의 공식에서 유도되었으며, 다음과 같은 두 가지 가정을 추가했다.
1. X선은 양자수 1과 2의 에너지 준위 사이의 전이에서 발생한다.
2. 수소보다 무거운 원자의 경우, 원자 번호 Z 대신 (Z-1)을 사용해야 한다. 이는 내부 전자에 의한 핵 전하 가림 효과 때문이다.
모즐리는 자신의 결과를 이론적으로 설명하기 어려워 보어에게 편지를 보냈지만, 당시 보어는 이 현상을 설명할 수 없었다. 이후 내부 껍질에 전자가 2개만 존재한다는 사실이 밝혀지면서 전하 가림 효과로 설명되었다.
모즐리의 법칙에 따르면, 두 번째 껍질에서 첫 번째 껍질로 전자가 이동할 때 방출되는 에너지(K-알파 선)는 다음과 같다.
::
또는
::
여기서 '''''R''v'''는 뤼드베리 상수로, 3.28 x 1015 Hz이다.
모즐리의 법칙은 원자 번호의 객관적인 의미를 확립하고, 러더퍼드-반 덴 브루크-보어 원자 모형의 타당성을 입증하는 데 기여했다.[58]
7. 한계 및 개선
보어 모형은 수소 원자의 스펙트럼은 잘 설명하지만, 다전자 원자의 스펙트럼을 정확하게 예측하지 못한다. 또한 전자가 특정 궤도를 따라 운동한다는 가정은 불확정성 원리에 위배된다. 그 밖에도 보어 모형은 다음과 같은 한계점들을 가지고 있다.[41]
- 더 큰 원자의 스펙트럼 대부분을 설명하지 못한다.
- 스펙트럼 선의 상대 강도를 제대로 예측하지 못한다.
- 스펙트럼 선의 미세 구조와 초미세 구조를 설명하지 못한다.
- 제만 효과를 설명하지 못한다.
- 이중선과 삼중선이 일부 원자의 스펙트럼에 매우 가까운 쌍으로 나타나는 이유를 설명하지 못한다.
- 다전자 원자는 이 모형에 의해 예측된 에너지 준위를 가지고 있지 않다. (중성) 헬륨에는 작동하지 않는다.
이러한 한계점들을 보완하기 위해 여러 개선된 모형들이 제시되었다.
7. 1. 좀머펠트의 개선 (보어-좀머펠트 모형)
보어 모형에 대한 여러 가지 개선이 제안되었는데, 가장 주목할 만한 것은 좀머펠트 또는 보어-좀머펠트 모형이었다. 이 모형은 전자가 보어 모형의 원형 궤도 대신 원자핵 주위를 타원 궤도로 이동한다는 것을 제안했다.[1] 이 모형은 보어 모형의 양자화된 각운동량 조건에 윌슨-좀머펠트 양자화 조건이라는 추가적인 방사형 양자화 조건을 보완했다.[42][43]
:
여기서 ''pr''은 좌표 ''qr''(즉, 방사형 위치)와 정준적으로 켤레인 방사형 운동량이고, ''T''는 하나의 완전한 궤도 주기이다. 이 적분은 작용의 작용-각 좌표이다. 대응 원리에 의해 제안된 이 조건은 양자수가 단열 불변량이기 때문에 가능한 유일한 조건이다.
보어-좀머펠트 모형은 근본적으로 불일치하고 많은 역설을 야기했다. 자기 양자수는 ''xy'' 평면에 대한 궤도 평면의 기울기를 측정했으며, 몇 가지 불연속적인 값만 취할 수 있었다. 이것은 원자가 좌표에 대해 제한 없이 어떤 방향이라도 가질 수 있다는 명백한 사실과 모순되었다. 좀머펠트 양자화는 서로 다른 정준 좌표에서 수행될 수 있으며 때때로 다른 답을 제공했다. 복사 보정의 통합은 복사/원자 결합 시스템에 대한 작용-각 좌표를 찾는 것이 필요하기 때문에 어려웠는데, 복사가 방출될 수 있을 때는 어렵다. 전체 이론은 비적분 운동으로 확장되지 않았는데, 이는 많은 시스템이 원칙적으로도 처리될 수 없다는 것을 의미했다. 결국, 이 모형은 1925년 볼프강 파울리가 하이젠베르크의 행렬 역학을 사용하여 처음 제시한 수소 원자의 현대적인 양자 역학적 처리로 대체되었다. 수소 원자의 현재 그림은 1926년 에르빈 슈뢰딩거가 개발한 파동 역학의 원자 궤도를 기반으로 한다.
그러나 보어-좀머펠트 모형이 성공하지 못한 것은 아니다. 보어-좀머펠트 모형을 기반으로 한 계산은 더 복잡한 원자 스펙트럼 효과를 정확하게 설명할 수 있었다. 예를 들어, 1차 섭동까지 보어 모형과 양자 역학은 슈타르크 효과에서 스펙트럼 선 분열에 대해 동일한 예측을 한다. 그러나 고차 섭동에서 보어 모형과 양자 역학은 다르며, 고전압 하에서 슈타르크 효과의 측정은 보어 모형보다 양자 역학의 정확성을 확인하는 데 도움이 되었다. 이러한 차이점의 주요 이론은 전자의 궤도 모양에 있으며, 이는 전자의 에너지 상태에 따라 다릅니다.
보어-좀머펠트 양자화 조건은 현대 수학에서 질문을 야기한다. 일관된 반고전 양자화 조건은 위상 공간에 특정 유형의 구조를 필요로 하는데, 이는 양자화할 수 있는 사교 다양체의 유형에 위상 제한을 둔다. 특히, 사교 형식은 에르미트 선다발의 연결의 곡률 형식이어야 하는데, 이를 전양자화라고 한다.
보어는 또한 1922년에 그의 모형을 업데이트하여 특정 수의 전자(예: 2, 8, 18)가 안정적인 "폐각"에 해당한다고 가정했다.[44]
8. 화학 결합 모델
닐스 보어는 원자 모형과 화학 결합 모형을 제안했다. 그의 이원자 분자 모형에 따르면, 분자를 구성하는 원자의 전자는 분자 축에 수직이고 원자핵으로부터 같은 거리에 있는 회전 고리를 형성한다. 분자계의 동적 평형은 핵이 전자 고리 평면을 끌어당기는 힘과 핵의 상호 반발력 사이의 힘 균형을 통해 달성된다. 보어의 화학 결합 모형은 쿨롱 반발력을 고려했는데, 고리의 전자는 서로 최대 거리에 있다.[45][46]
참조
[1]
논문
Models and Modelers of Hydrogen
[2]
논문
Les Hypothèses moléculaires
https://fr.wikisourc[...]
[3]
논문
Niels Bohr's Second Atomic Theory
1979-01-01
[4]
간행물
Before Bohr: Theories of atomic structure 1850-1913
https://css.au.dk/fi[...]
Centre for Science Studies, University of Aarhus
2010-10-01
[5]
서적
The tiger and the shark: empirical roots of wave-particle dualism
Cambridge Univ. Press
1992
[6]
서적
Niels Bohr: a centenary volume
https://archive.org/[...]
Harvard University Press
1985
[7]
논문
The Scattering of α and β Particles and Rutherford's Atom
https://www.jstor.or[...]
1968-01-01
[8]
논문
I. On the constitution of atoms and molecules
https://zenodo.org/r[...]
1913-07-01
[9]
서적
Niels Bohr and the Quantum Atom: The Bohr Model of Atomic Structure 1913–1925
Oxford University Press
2012
[10]
논문
VII. On electrical vibrations and the constitution of the atom
https://zenodo.org/r[...]
1906-01-01
[11]
서적
A history of the theories of aether & electricity. 2: The modern theories, 1900 - 1926
Dover Publ
1989
[12]
논문
Atomic Theory and Mechanics1
https://www.nature.c[...]
1925-12-01
[13]
서적
From data to quanta: Niels Bohr's vision of physics
The University of Chicago press
2021
[14]
인터뷰
Niels Bohr – Session III
https://www.aip.org/[...]
American Institute of Physics
1962-11-07
[15]
논문
The Genesis of the Bohr Atom
1969-01-01
[16]
논문
The path to the quantum atom
2013-06-01
[17]
서적
Old Quantum Theory and Early Quantum Mechanics. Challenges in Physics Education.
https://link.springe[...]
Springer Nature Switzerland
2024
[18]
논문
The atomic theory of John William Nicholson
1966-01-01
[19]
논문
The Constitution of the Solar Corona. IL
Oxford University Press
1912-06-14
[20]
서적
On the Constitution of Atoms and Molecules ... Papers of 1913 reprinted from the Philosophical Magazine, with an introduction by L. Rosenfeld
Copenhagen; W.A. Benjamin: New York
1963
[21]
서적
Quantum Reality, Relativistic Causality, and Closing the Epistemic Circle
Springer
2009
[22]
서적
The Age of Entanglement
[23]
잡지
Revealing the hidden connection between pi and Bohr's hydrogen model
http://physicsworld.[...]
2015-11-17
[24]
논문
Positron production in crossed beams of bare uranium nuclei
http://nbn-resolving[...]
1988-03-01
[25]
서적
Collected works
North-Holland Publ. Cy.
1985
[26]
서적
Inward bound: of matter and forces in the physical world
Clarendon Press [u.a.]
2002
[27]
논문
I. On the constitution of atoms and molecules
https://www.tandfonl[...]
1913-07-01
[28]
서적
The quantum story: a history in 40 moments
Oxford Univ. Press
2013
[29]
논문
Early atomic models – from mechanical to quantum (1904–1913)
https://link.springe[...]
2013-01-01
[30]
논문
On the Constitution of Atoms and Molecules, Part II. Systems containing only a Single Nucleus
1913-01-01
[31]
논문
LXXIII. On the constitution of atoms and molecules
https://zenodo.org/r[...]
1913-11-01
[32]
논문
The Constitution of Atoms and Molecules
https://zenodo.org/r[...]
1914-05-01
[33]
논문
Langmuir's Theory of the Arrangement of Electrons in Atoms and Molecules
https://zenodo.org/r[...]
1921-07-01
[34]
논문
Über Molekülbildung als Frage des Atombaus
https://zenodo.org/r[...]
1916-01-01
[35]
논문
Lars Vegard, atomic structure, and the periodic system
http://acshist.scs.i[...]
2012-01-01
[36]
저널
The Arrangement of Electrons in Atoms and Molecules
https://zenodo.org/r[...]
1919-06-01
[37]
인터뷰
Niels Bohr – Session I
https://www.aip.org/[...]
American Institute of Physics
1962-10-31
[38]
저널
The high-frequency spectra of the elements
https://archive.org/[...]
1913-01-01
[39]
저널
The Bohr–Moseley synthesis and a simple model for atomic x-ray energies
[40]
저널
Die Radioelemente, das periodische System und die Konstitution der. Atome
https://babel.hathit[...]
1913-01-01
[41]
저널
Wigner's phase space function and atomic structure: I. The hydrogen atom ground state
1982-12-10
[42]
저널
Zur Quantentheorie der Spektrallinien
https://zenodo.org/r[...]
[43]
저널
The quantum theory of radiation and line spectra
https://zenodo.org/r[...]
[44]
서적
The Life of Stars: The Controversial Inception and Emergence of the Theory of Stellar Structure
Springer
[45]
서적
Избранные научные труды (статьи 1909–1925)
«Наука»
[46]
저널
Bohr's 1913 molecular model revisited
2005-08-23
[47]
서적
Compendium of quantum physics: concepts, experiments, history, and philosophy
Springer
2009
[48]
웹사이트
Logo Usage Guidelines
https://www.iaea.org[...]
2024-09-04
[49]
문서
長岡半太郎の原子模型を発展させたものであるといわれる。
[50]
참고자료
[51]
참고자료
[52]
저널
On the Constitution of Atoms and Molecules, Part I
http://web.ihep.su/d[...]
[53]
웹인용
Olsen and McDonald 2005
http://www.physics.p[...]
2020-11-11
[54]
웹사이트
CK12 – Chemistry Flexbook Second Edition – The Bohr Model of the Atom
http://www.ck12.org/[...]
2014-09-30
[55]
서적
Quantum Reality, Relativistic Causality, and Closing the Epistemic Circle
Springer
2009
[56]
서적
The Age of Entanglement
2009
[57]
웹사이트
Interview of Niels Bohr by Thomas S. Kuhn, Leon Rosenfeld, Erik Rudinger, and Aage Petersen
http://www.aip.org/h[...]
Niels Bohr Library & Archives, American Institute of Physics
2019-03-27
[58]
저널
The Bohr–Moseley synthesis and a simple model for atomic x-ray energies
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
